两元一次方程组的解法公式法详解
在数学的世界中,方程组是解决实际问题的重要工具。尤其是两元一次方程组,它不仅在学术研究中占有一席之地,更在日常生活中频繁出现。无论是经济学中的供需分析,还是工程学中的资源分配,掌握两元一次方程组的解法都显得尤为重要。本文将详细介绍两元一次方程组的解法公式法,帮助读者更好地理解和应用这一数学工具。
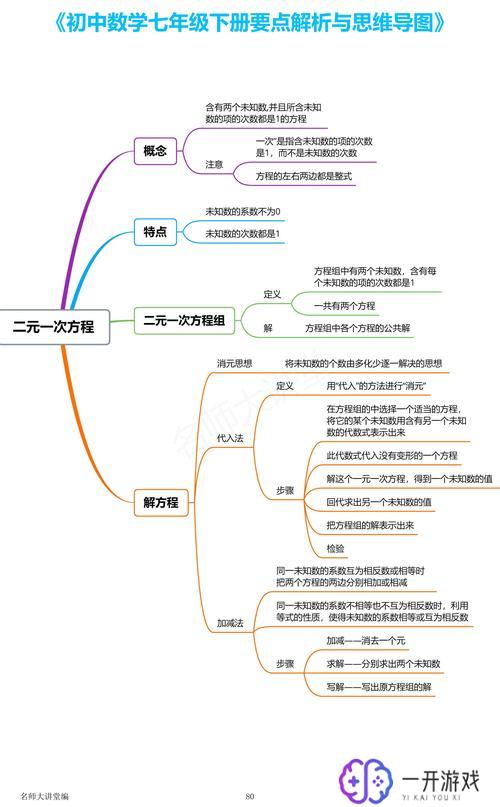
什么是两元一次方程组?
两元一次方程组是由两个方程组成的方程组,每个方程中包含两个未知数,且每个未知数的最高次数为一。一般形式为:
ax + by = c
dx + ey = f
其中,a、b、c、d、e、f为常数,x和y为未知数。解决这个方程组的目标是找到x和y的值,使得两个方程成立。
公式法解两元一次方程组
公式法是解决两元一次方程组的一种有效方法,通常使用代入法或消元法。这里我们主要介绍消元法的公式解法。
消元法步骤
消元法的基本思想是对方程进行加减运算,消去一个未知数,从而将方程组转化为一个单一的方程。具体步骤如下:
- 将方程组标准化,确保每个方程的形式为ax + by = c。
- 选择一个方程,利用加减法消去一个未知数。例如,可以将第一个方程乘以一个适当的系数,使得y的系数相同,然后相减。
- 得到一个只含有x的方程,解出x的值。
- 将x的值代入任一原方程,解出y的值。
示例解析
假设我们有以下方程组:
二x + 三y = 六
四x - y = 五
我们可以将第一个方程乘以一,第二个方程乘以三,使得y的系数相同:
二x + 三y = 六
一十二x - 三y = 一十五
接下来,将两个方程相加:
一十四x = 二十一
解出x的值:
x = 一.五
然后,将x的值代入第一个方程:
二(一.五) + 三y = 六
三 + 三y = 六
三y = 三
y = 一
因此,方程组的解为:(x, y) = (一.五, 一)。
以上的分析,我们可以看到,利用公式法解两元一次方程组是一种高效且系统的方法。掌握这一方法,不仅能够帮助我们解决数学问题,还能在实际生活中应用到各种场景。希望本文能够帮助读者更深入地理解两元一次方程组的解法,提升数学思维能力。



















