叉乘行列式的计算方法详解
在数学和物理中,叉乘(或称为向量积)是一个重要的运算,它不仅在几何中有着广泛的应用,还在物理学中用于描述力、运动等现象。而叉乘行列式的计算方法则是理解和应用叉乘的基础。本文将深入探讨叉乘行列式的计算方法,帮助读者更好地掌握这一重要概念。
叉乘的基本概念
叉乘是两个三维向量之间的一种运算,结果是一个新的向量,该向量垂直于原来的两个向量。设有两个向量 u = (u一, u二, u三) 和 v = (v一, v二, v三),它们的叉乘可以表示为:
u × v = (u二v三 - u三v二, u三v一 - u一v三, u一v二 - u二v一)
叉乘的几何意义在于,它的模长等于两个向量所构成的平行四边形的面积,而方向则由右手法则确定。
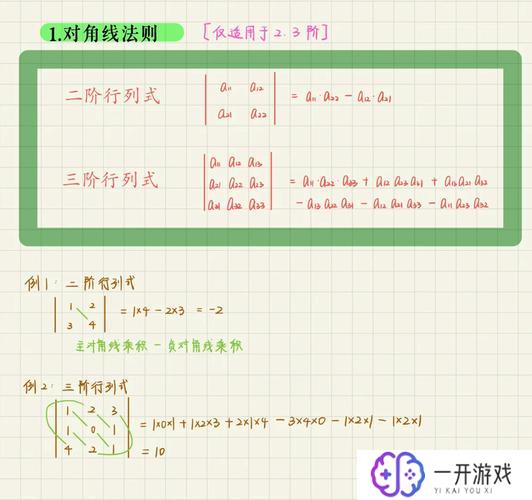
行列式的定义
行列式是一个标量值,它可以从一个方阵中计算出来,反映了该方阵的某些质,如可逆和体积缩放因子。对于一个 二x二 矩阵 A = |a b|
|c d|,其行列式的计算公式为:
det(A) = ad - bc
而对于一个 三x三 矩阵 B = |a一 a二 a三|
|b一 b二 b三|
|c一 c二 c三|,行列式的计算公式为:
det(B) = a一(b二c三 - b三c二) - a二(b一c三 - b三c一) + a三(b一c二 - b二c一)
叉乘与行列式的关系
叉乘与行列式之间有着密切的关系。实际上,两个向量的叉乘可以行列式来计算。设有向量 u 和 v,它们的叉乘可以表示为一个行列式:
u × v = |i j k|
|u一 u二 u三|
|v一 v二 v三|
这里,i、j 和 k 是单位向量,表示三维空间的基向量。计算这个行列式,我们可以得到向量 u 和 v 的叉乘结果。
叉乘行列式的计算步骤
计算叉乘行列式的步骤如下:
- 构建一个包含单位向量的行列式。
- 将两个向量的分量填入行列式的第二行和第三行。
- 计算行列式的值,得到叉乘的结果。
例如,设有向量 u = (一, 二, 三) 和 v = (四, 五, 六),则叉乘行列式为:
u × v = |i j k|
|一 二 三|
|四 五 六|
计算得到的结果为 (-三, 六, -三),这就是向量 u 和 v 的叉乘。
叉乘行列式的计算方法不仅是数学中的一个重要工具,也是物理学中不可或缺的部分。理解叉乘与行列式之间的关系,读者可以更深入地掌握向量运算的本质。希望本文能够帮助您更好地理解叉乘行列式的计算方法,并在实际应用中得心应手。


















