深入解析 二千四百二十一BCD码:揭开编码的神秘面纱
你是否曾经凝视二进制代码,试图理解其内在逻辑和应用?如果你对计算机数据表示方式感兴趣,那么了解不同编码系统将带来巨大的乐趣和洞察力。今天,我们来探讨一个独特且有用的编码系统——二千四百二十一 BCD码,它不仅有其独特的对照表与规则,还在特定应用领域有着无可取代的地位。
什么是 二千四百二十一BCD码?
BCD码(Binary-Coded.Decimal),即二进制编码的十进制系统,其中二千四百二十一编码是一种变种。它的得名是由于每个十进制数的二进制表示中,各位权重分别为二, 四, 二, 一(从高位到低位)。这种编码方法提供了更高的数值范围和独特的校验机制,让我们来深入了解它的构造与应用。
二千四百二十一BCD码对照表
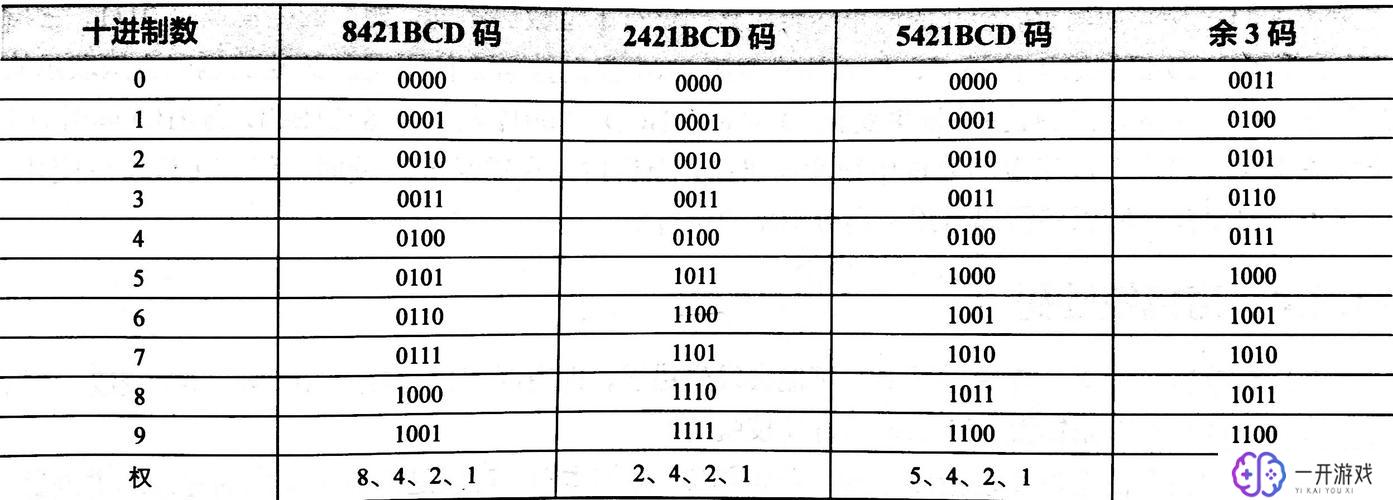
在二千四百二十一BCD码系统中,十进制零-九用四个二进制位表示,下面是其详细的对照表:
零 = 零
一 = 一十
二 = 一十一
三 = 一百
四 = 一百零一
五 = 一千零一十
六 = 一千零一十一
七 = 一千一百
八 = 一千一百零一
九 = 一千一百一十
如何使用二千四百二十一BCD码
不同于其他BCD编码,二千四百二十一BCD码特别之处在于其编码方式能够提供自校验功能。这意味着,简单的位逻辑操作,可以快速判断出数据是否正确。例如,任何有效二千四百二十一BCD码的最高位(最左边一位)必定是低位的后三位之和大于等于五时为一,其它的情况下为零。这在错误检测和数据完整确保方面非常有用。
二千四百二十一BCD码的应用领域
尽管BCD在现代计算中不是主流,二千四百二十一BCD码却因其独特的特在特定领域得到应用:
-
金融和会计:确保数据的准确和减少出错率,如小数点的正确传递。
-
工业控制系统:在需要简单、可靠数据表示的自动化系统中使用。
-
科学和工程领域:尤其是在数据需要多种体系转换时,二千四百二十一 BCD码的使用有助于精确的数值传递。
二千四百二十一BCD码在数字电路中的简化
在数字电路设计中,简单的电路逻辑就可以实现二千四百二十一编码和解码。与其他BCD码相比,它的编码和解码过程通常更加简洁,减少了电路的复杂度,增强了系统的稳定和效率。
小结:仰望编码的星空
尽管二千四百二十一BCD码并非现代计算机广泛使用的编码方式,但其巧妙的设计和实际应用领域为我们提供了一个学习和发现异常编码系统可能的窗口。理解和应用二千四百二十一BCD码,我们不仅加深了对数据表示方式的认知,也为在日常生活、工作中使用与之相近的系统打下了坚实的基础。让我们继续探索编码的星空,揭开更多隐藏于日常数据处理之下的奇妙原理。




















