行列式的计算质详解
在数学的世界中,行列式是线代数中一个重要的概念。它不仅在理论上具有深远的意义,而且在实际应用中也扮演着不可或缺的角色。无论是在解线方程组、计算矩阵的逆,还是在多元微积分中,行列式都展现出了其独特的价值。本文将深入探讨行列式的计算质,帮助读者更好地理解这一重要工具。
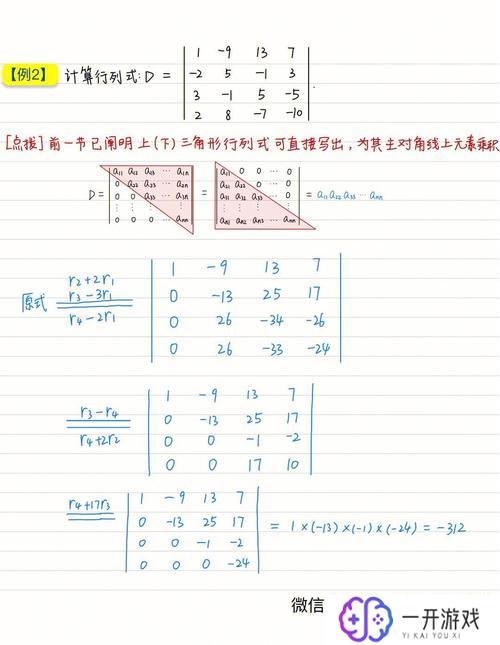
行列式的基本定义
行列式是一个与方阵相关的标量值,通常用符号 det(A) 表示,其中 A 是一个 n × n 的方阵。行列式的值可以多种方法计算,包括递归展开法、行列变换法等。行列式的值不仅反映了矩阵的某些质,如可逆和线相关,还在几何上表示了由矩阵列向量所张成的 n 维体积。
行列式的计算质
行列式的计算质可以归纳为以下几个重要方面:
1. 交换行或列
如果交换矩阵的任意两行或两列,则行列式的值会发生改变,变号。即:det(A) = -det(B),其中 B 是交换 A 的两行或两列得到的矩阵。这一质在行列式的计算中非常重要,尤其是在简化计算时。
2. 行或列的倍数
如果将矩阵的某一行或某一列乘以一个常数 k,则行列式的值也会乘以 k。即:det(kA) = k * det(A)。这意味着在计算行列式时,可以适当的行列变换来简化计算过程。
3. 行或列的线组合
如果将矩阵的某一行或某一列替换为该行或列与其他行或列的线组合,则行列式的值不变。即:det(A) = det(B),其中 B 是线组合得到的矩阵。这一质使得在计算行列式时,可以消元法等手段简化矩阵。
4. 行列式的乘法质
对于两个 n × n 的矩阵 A 和 B,有以下质:det(AB) = det(A) * det(B)。这意味着行列式的计算可以分解矩阵的乘法来简化,尤其是在处理大规模矩阵时。
5. 单位矩阵的行列式
单位矩阵的行列式值为 1,即:det(I) = 1。这一质为计算其他矩阵的行列式提供了基准。
6. 零行列式
如果矩阵 A 的某一行或某一列全为零,则其行列式的值为零,即:det(A) = 0。这表明矩阵不可逆,且其列向量线相关。
行列式的计算质为我们提供了强大的工具,使得在处理线代数问题时更加高效。理解和运用这些质,我们可以更轻松地计算行列式,并在实际应用中发挥其重要作用。希望本文能够帮助读者更深入地理解行列式的计算质,为今后的学习和研究打下坚实的基础。



















